Omicron

It occurred to me that the talk of perhaps bringing in restrictions some time in the future was probably poorly timed, in that we are probably pretty close to the peak right now and if action is going to be worthwhile, it needs to be pretty much immediate. Having made a few comments to that end on twitter, I thought I should check out my intuition with some calculations. So here they are.

My starting point is that the Omicron variant represented 22% of tests on the 11th Dec (link) and we had about 40k positive tests on that day (link - but see additional note at bottom of post) meaning 9k tested cases which I will assume represents 18k real infections (ie 50% of infections are actually observed) and furthermore I'll assume that these infections happened on the 8th as it must take a little while to feel ill and get tested. 

I'm using a doubling time of about 2 days with an underlying R0 number of 6, and another assumption I'm making is that the population is about 50% immune. I'm ignoring the Delta infection which is small in comparison and carries on largely in parallel with Omicron.

So I initialise the model to hit 18k infections on the 8th, and ran it forwards. This is what I get with no action at all, just the natural infection profile of an uncontrolled epidemic:

32 million infections in total, with a daily peak of 2.7 million on the 27th.

If instead we were to introduce severe restrictions now, such that the underlying R0 dropped from 6 to 1.5, the epidemic would be much smaller:

A daily max of about 430k infections and only 4 million in total. Note that the underlying R0 dropping to 1.5 means the effective R value drops to about 0.75 as the population is half immune.

However the Govt seems to be slowly meandering towards the possibility of some restrictions in about a week. If we were to say Boxing Day instead, then we get:

The daily max here is 2.4 million, with the total about 16 million. So even this delayed action does cut the epidemic in half, by shutting it down rapidly from the peak. That's a bit better than my intuition had suggested to me.

The details of these calculations are sensitive to the timing of the peak of course, which depends on all the assumptions I've made. What is not in doubt is that every day makes quite a big difference to the outcome.

Edit: In the time it took me to write this post, the number of cases by specimen date on the 11th has been updated to 46k!

More COVID

Posting this mostly because some people seem to be under the misapprehension that the UK is doing really well at coping with COVID, at least in comparison to our European neighbours. It's simply not true, though it's hard to discern quite how poorly we are doing from most of the media including the BBC. This article in the FT presents some of the data, and I'll take some more from OWID.

While the rapid start of the vaccination campaign was certainly impressive and genuinely superior to the rest of the EU, we have now been overtaken by many of our neighbours.

That's us 2nd from bottom on that chart of major European nations.

Vaccination of children has been abysmal, both with the stupid delay due to JCVI's shilly-shallying, and then the slow roll-out. Boosters are running at about half the rate that the original vaccination was, so the backlog is growing rapidly.

 

Our own volunteer-run vacc centre was mothballed a while back, we could be doing a thousand a day no problem, but it's apparently not part of the plan.

Case numbers are far higher here than just about anywhere else in Europe. USA is comparable, which is hardly an endorsement.

And of course plenty of deaths too:

Yes, both France and Spain had a bit of bump in the late summer, but quickly got on top of it, which we haven't bothered to do. There's no sign of any improvement and in fact the recent case numbers are ticking up quite firmly, so we can probably expect deaths to follow. The deaths aren't really the only problem of course, the knock-on effect of pressure on the hospitals affects a much broader range of people who aren't even infected.

In case you are thinking optimistically that just about everyone must have had it by now and the numbers must be about to go down, I've seen it said that some regions of Iraq, the total number of cases to date is substantially higher than the population, i.e. many people have had it twice or more. Immunity doesn't last. Of course the severity of the disease is far lower after vaccination, and hopefully will also drop with prior infection. But it's not going to go away and the reluctance of the govt to take any action to help control the disease probably means we'll be stuck with very high levels for the foreseeable future.

Speed vs power in Zwift

This may be of interest to a relatively small number of readers, but it seems worth documenting that the relationship between power and equilibrium flat speed in the cycling simulator Zwift can be quite accurately summarised via 

P =  1.86e-02 w.v - 5.37e-04 v^3 + 2.23e-05 w.v^3 + 1.33e-05 h.v^3

where v is the velocity in kph, w is the rider weight in kg, and h is the rider height in cm.

The linear term in v can be thought of as arising through rolling resistance (which also varies with w), with the three cubic terms due to air resistance. These cubic terms can be thought of as the dominant terms in a Taylor series expansion of a single term that looks like A.f(w,h).v^3 where f is a function of weight and height that modifies the resistance (eg though changing the cross sectional area). At first I was trying to work out what f was, but an important realisation that only came to me while doing this analysis is that I don't actually need to know its form as the values of w and h only deviate moderately from their mean values for the practical range of riders I'm interested in (ie ± 10% the most part, 20% at worst). Therefore this linearisation approach (with coefficients fitted through linear regression) is plenty good enough and I don't need any of my model-fitting tricks. More engineering than science but nevertheless useful!

To do the model fitting, I did a bunch of flying laps of the volcano circuit at constant power, with different physical parameters and varying power level each time. This route is fairly flat but not perfectly so, which means the average speed here will be a little bit lower than that achieved on truly flat ground, but probably typical of many flattish routes on Zwift such as Watopia's Waistband or Greater London Flat. I estimate the elevation/disequilibrium effect here to be around 0.5kph, so speeds achieved on Tempus Fugit may be about that much quicker than indicated here (or conversely, you'll hit a target pace with a bit less power than this formula suggests). Some of the riders in my data set are real, others imaginary. I've focussed mostly on women, first because I've been DS for my wife's team for a while, and also because through being a large reasonably fit man I can generate their racing power fairly comfortably for long enough to get a fix on their speeds. (Yes, I know there are software approaches to simulating the power. But it's something else to set up, and I don't really want to get into the world of power bots, you never know where it might lead...) Calculating the power needed for a large rider at high speed requires a bit of an extrapolation and may get less reliable. Bike is the Tron, I started out testing different bikes (to check on what zwiftinsider says) but the differences were too trivial to pursue. Specifically, the Canyon Aeroad 2021 with Zipp 808 wheels which I used to use a lot was just one second slower than the Tron. That's 0.1kph, equivalent to less than 2W.

The black lines in the plot below are the model predictions for each rider, with the crosses marking the data points that I used to fit the model. Each line has 3 data points except for the top one which is my own physics. If someone wants to do a flying lap of the volcano at 450W (using my physical parameters) I'd love to know the result :-) The rest are mostly based around a women's team with jules being the bottom line. Few cyclists of either gender lie outside the range of our parameters! The model-data residuals are about 1.5W on average (RMS error) which is basically the magnitude of measurement error on the speed which is only precise to 0.1kph. This level of precision is plenty good enough for practical use, it's difficult to hit a power target more closely than about 5W anyway.

A conclusion that may be drawn is that for a medium-sized cyclist riding around 42kph, an extra 1kg of weight requires 2.5W more power to maintain the same speed (or alternatively, 1kg less saves 2.5W of power). For an additional 1cm of height, it's around 1W. These numbers aren't far from what I'd estimated through experience, it's nice to have them confirmed in a more careful calculation.

History in the (re)making?

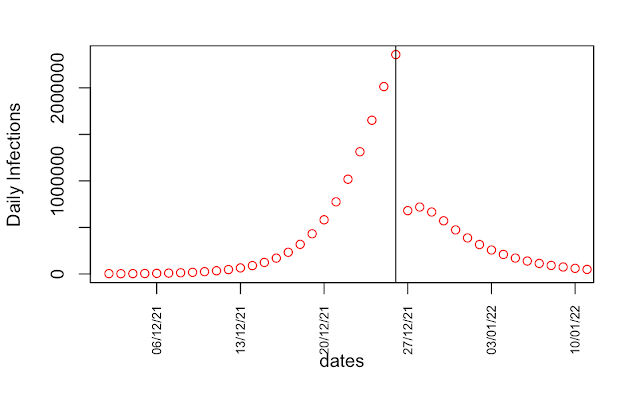
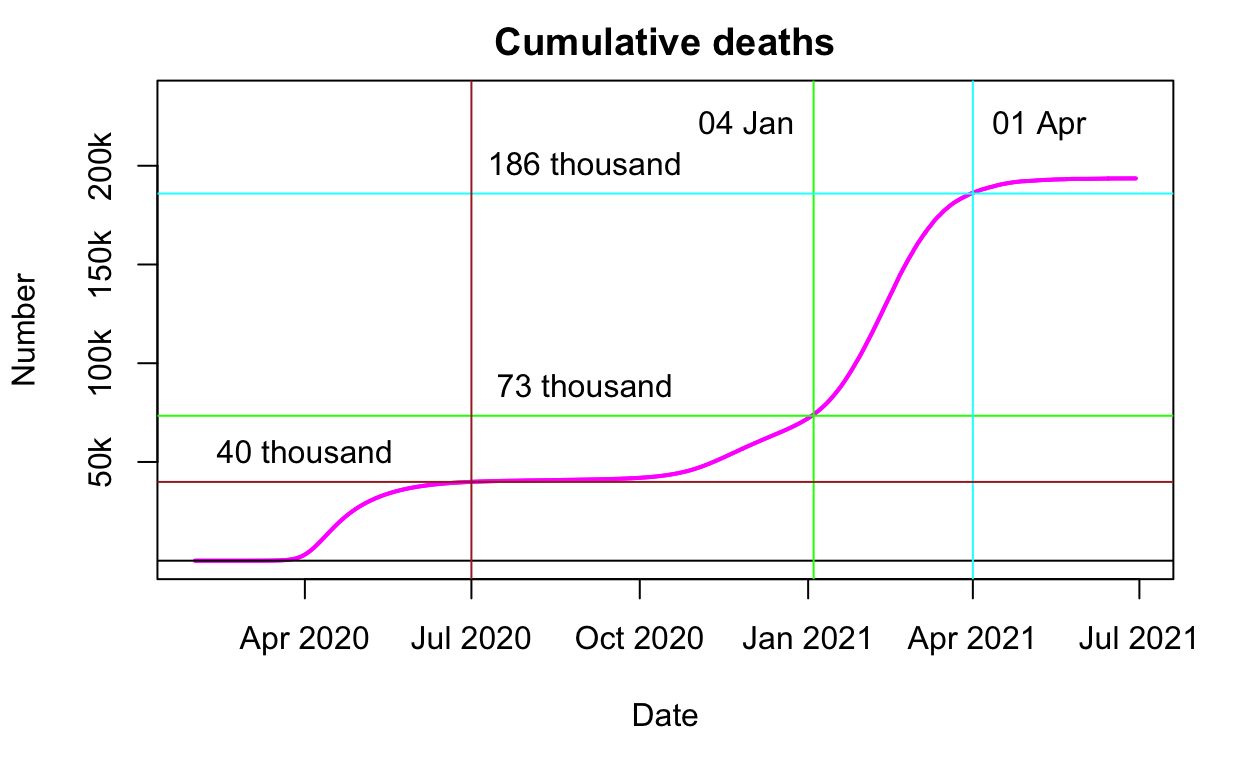
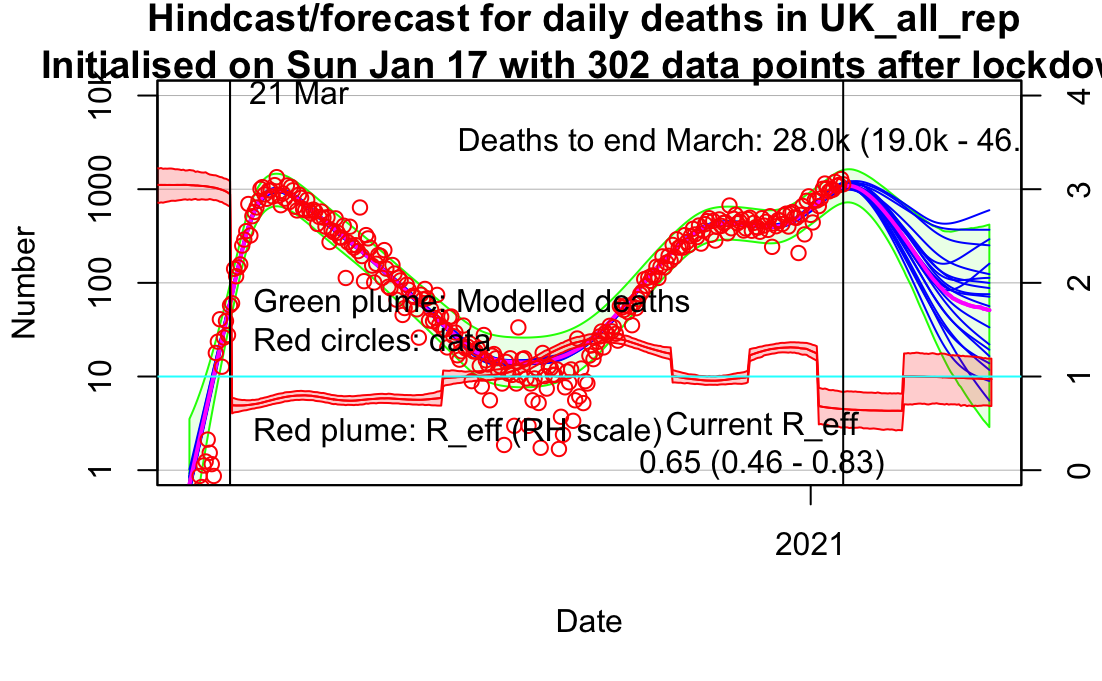
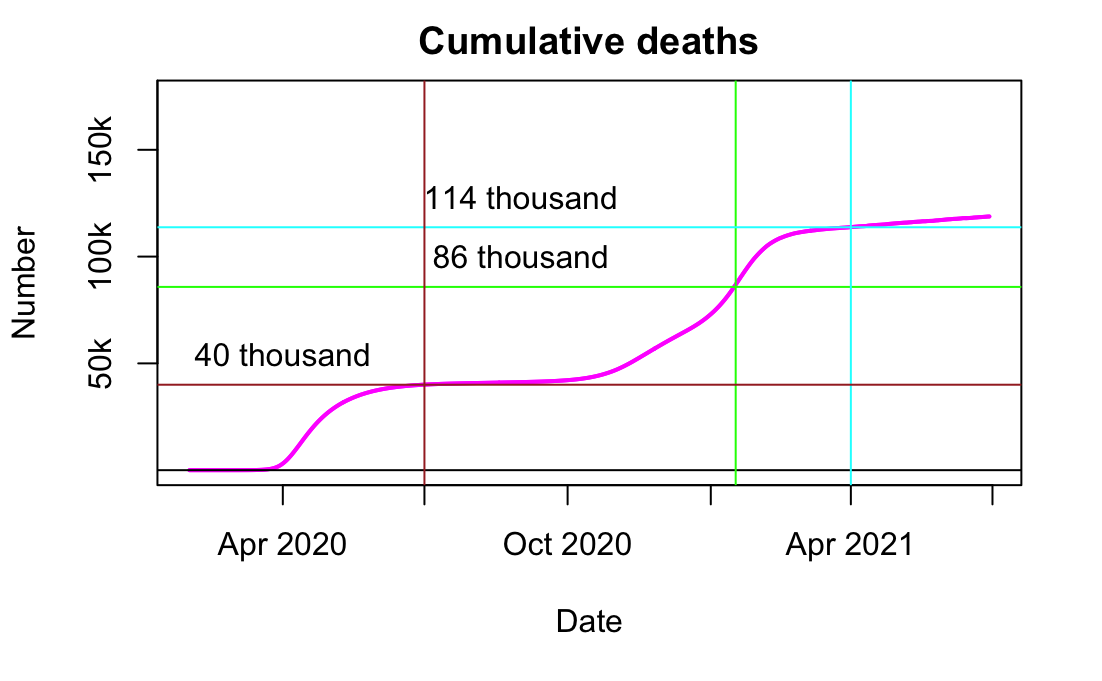
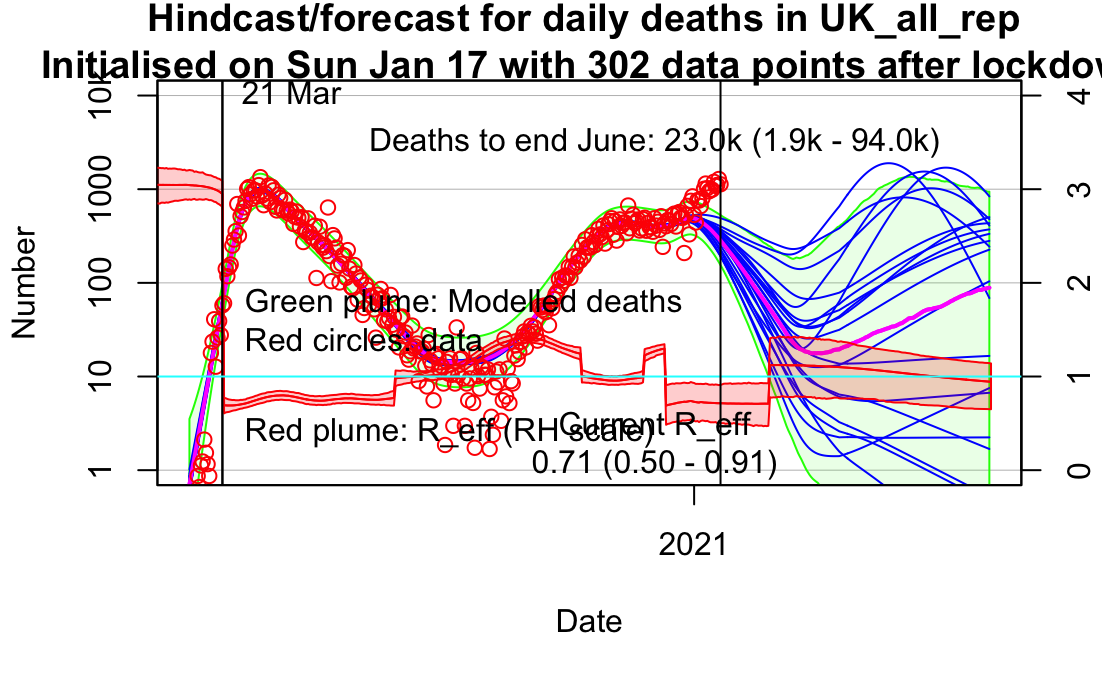
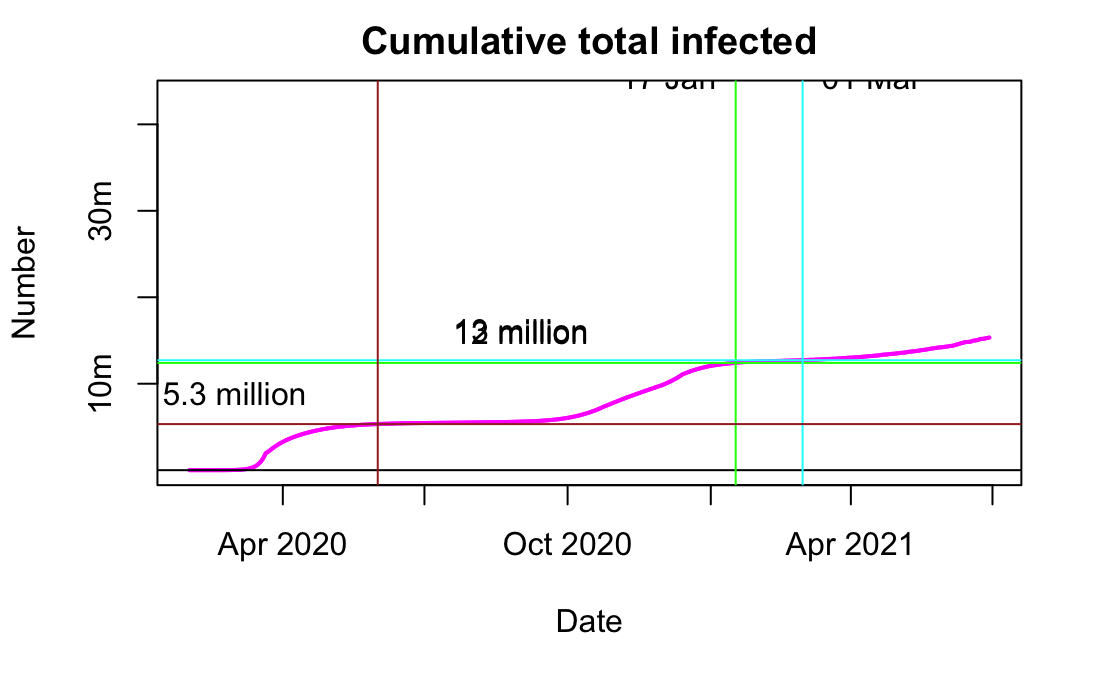
One year on and there's been a slew of articles revisiting the events of the past year. I was going to ask what has prompted this little flurry, but it's obviously the anniversary thing. With increasing pressure for a public inquiry, it seems that some of the key players have been trying to position themselves favourably, so let's have a look at what's been written, versus what the contemporaneous documentation actually says. SAGE minutes can be found here, I think (I downloaded the relevant docs a while back).

The first article I noticed was Laura Kuenssberg's “Inside Story”. She “talked to more than 20 of the people who made the life and death decisions on Covid”. The relevant passage that I am interested in concerns the decision making around mid-March:

“13 March, the government's Scientific Advisory Group for Emergencies (Sage) committee concluded the virus was spreading faster than thought.

But it was Downing Street "modellers in the building", according to one current official, who pored again over the numbers, and realised the timetable that had only just been announced was likely to result in disaster.

The next morning, a small group of key staff got together. Simple graphs were drawn on a whiteboard and the prime minister was confronted with the stark prediction that the plan he had just announced would result in the NHS collapsing under the sheer number of cases.

Several of those present tell me that was the moment Mr Johnson realised the urgency - that the official assumptions about the speed of the spread of this new disease had been wrong.

[...]

On 16 March, the public were told to stop all unnecessary social contact and to work at home if possible.

[...]

For many inside government, the pace of change that week was staggering - but others remain frustrated the government machine, in their view, had failed to move quickly enough.”

The narrative being presented here of ponderous government is significantly misleading.

The govt claimed at the time to be paying close attention to the scientific advice from SAGE, and the specific change to SAGE's assessment on the 13th March was not that the disease was spreading any more rapidly, but merely that the number of infections was higher than previously thought (due to greater importation from abroad). This is a key distinction that anyone numerate should be able to grasp readily. To quote from SAGE minutes on the 13th:

“Owing to a 5-7 day lag in data provision for modelling, SAGE now believes there are more cases in the UK than SAGE previously expected at this point, and we may therefore be further ahead on the epidemic curve, but the UK remains on broadly the same epidemic trajectory and time to peak. 

[...]

SAGE was unanimous that measures seeking to completely suppress spread of Covid- 19 will cause a second peak.”

Changing the estimate of the number of cases just brings the peak forward by a few days. Even a factor of 2 is only a single doubling time which they thought to be about 5-7 days at that time. Changing the estimate of the growth rate could (and in fact did) change the timetable and urgency much more significantly, but this didn't happen for another week and a half.

It is not clear who “the modellers in the building” refers to in Kuenssberg's piece, but they are clearly not SAGE. Maybe Cummings had run a few numbers on a spreadsheet but since SAGE was supposed to be an assembly of world-leading experts, it would hardly be appropriate to discard their analyses in favour of his. For that matter, I had also blogged that the mitigation plan was likely to overwhelm the NHS (a conclusion that I reached around the 9th March based on some very simple calculations) but I wouldn't expect Johnson to listen to me either. SAGE minutes are very clear that they still believed the doubling rate to be 5-7 days right up to the 18th March and had described any overload on the NHS as being some way off (albeit a looming problem that would need addressing at some time in the future). They were unanimously (see above) opposed to suppression at this point.

On the 16th, the SAGE meeting changed its advice somewhat and suggested that some social distancing measures (but not school closures) should be implemented promptly:

“SAGE advises that there is clear evidence to support additional social distancing measures be introduced as soon as possible.

[...]

SAGE will further review at its next meeting whether, in the light of new data, school closures may also be required to prevent NHS capacity being exceeded.”

Clearly there was some increased urgency here but NOT any indication that the NHS was under immediate threat, in direct contradiction to Kuenssberg's unattributed claim above that “the prime minister was confronted with the stark prediction that the plan he had just announced would result in the NHS collapsing under the sheer number of cases.” I'm not saying it is impossible that anyone said such a thing, but if they did, they were an isolated voice and certainly not representative of SAGE as a whole.

Immediately following the SAGE meeting on the 16th, the Govt did of course request that people avoid all unnecessary social contact. Admittedly, this instruction had neither legal force nor economic support at that point but SAGE was obviously reasonably satisfied with the adequacy of this plan as can be seen from their minutes of the 18th (at which time they also recommended school closures):

“SAGE advises that the measures already announced should have a significant effect, provided compliance rates are good and in line with the assumptions. Additional measures will be needed if compliance rates are low.”

So it was only in the case of poor compliance that additional measures would be required.

There was no SAGE meeting between 18th and 23rd, which was unfortunate in the circumstances (21-22 being a weekend). On the 23rd, SAGE finally realised that they had got the R number wrong and that as a result the doubling time was much shorter than had been previously believed, making the situation quite desperate. Specifically, the SAGE meeting of the 23rd concluded: “Case numbers could exceed NHS capacity within the next 10 days on the current trajectory” and this statement must be understood in the context of the immediately preceding 20th March SPI-M meeting which noted both: “Any measures enacted would take 2-3 weeks to have an impact on ICU admissions” and also: “If the higher reproduction number is representative of the longer term, then it is likely that additional measures will be required to bring it below one”.

Thus SAGE's underestimate of the R number didn't just mean that the epidemic was coming faster and harder than previously thought: another consequence is that actions that would have been adequate for R=2.4, might not be adequate for R=3. It is quite understandable that this caused alarm within SAGE, but it only happened on the 23rd.

The Govt imposed a legally-enforceable lockdown with much more far-reaching restrictions immediately that evening (23rd March).

Moving on to the next article, in the Guardian, a hagiography of Patrick Vallance:

“But it now seems clear that Boris Johnson, and his advisers, were slow to heed Vallance’s early advice.

Before the 16 March press conference, Vallance chaired a meeting of the Scientific Advisory Group for Emergencies (Sage) in which a collection of experts had advised that the first lockdown should begin immediately.

Johnson did not announce the unprecedented national lockdown until a week later on 23 March in a primetime TV address to the nation.”

This is simply not true as documented above. SAGE asked for relatively modest action around the 16-18th, and the Govt responded promptly. SAGE explicitly assessed on the 18th that the actions were probably adequate and it was only on the 23rd when they realised that they had got the doubling time wrong, that they suddenly realised they had a much larger and more urgent problem on their hands. Vallance also got this wrong in his appearance before the House of Commons Select Committee on Science and Technology. 

Most recently, a podcast on the Guardian consisting of an interview of Neil Ferguson. He points very firmly to the data about higher case numbers due to greater importation being what drove the accelerated decision making in mid-March (NB this view is very different from Vallance who very emphatically linked the change in policy advice to the revision of the estimated doubling time - it is simply not possible for both Ferguson and Vallance to both be correct about this). Ferguson mentions this being discussed in the “first weekend in March” which I'm sure must be a simple slip as this would be 7-8th March whereas on the 10th and even 13th SAGE seems pretty sanguine about the situation and does not suggest any need to take immediate action. Assuming he meant the 14-15th March instead, this is far more consistent with SAGE as the minutes of the 16th do certainly suggest some some action should be taken in the light of the new data:

“The science suggests additional social distancing measures should be introduced as soon as possible.”

When asked specifically (at 11m20 in the podcast) “were scientists telling ministers to go earlier?” Ferguson firstly points again to the surveillance data as escalating the decision making process, and then coyly says it was entirely in the Govt's hands as to what actions they took. He could have said, but chose not to, that the Govt followed SAGE's advice promptly and to the letter. And the interviewer didn't pursue the point. While the improved surveillance data undoubtedly played a role in the process, the urgent advice for the most stringent controls only came on the 23rd as a result of the revised estimate of doubling time. You only have to glance at the SAGE minutes to see that they were not shy about offering policy advice throughout the outbreak.

At 16m40 onwards the interviewer says, with reference to the situation in September after schools reopened: 

“...once again the advice from scientists was to lock down. But that advice was not heeded. Did that delay once again lead to a higher death rate than we might have seen?”

Without getting into the September story here, any delayed response from the Govt (which I don't dispute was evident in the autumn) could only “once again” have resulted in a higher death rate if there had also been a delayed response to advice to lock down in March. Which there was not, according to the evidence I have outlined.

BlueSkiesResearch.org.uk: Escape velocity

There is currently lot of debate on how and when we lift restrictions, and the risks of this. There are several unknowns that may affect the outcome. I have extended the model in a couple of simple ways, firstly by including a vaccination effect which both immunises people, and substantially reduces the fatality rate of those who do get ill, and also by including a loss of immunity over time which is potentially important for longer simulations. The magnitudes of these effects seem highly uncertain, I’ve just made what seems like plausible guesstimates. I use a vaccination rate of 0.5% per day which is probably in the right ballpark though my implementation is extremely simplistic (NB this is the rate at which people move from the vulnerable to the immune category, so it directly accounts for the imperfect performance of the vaccine itself). As well as this, I’m assuming the fatality rate for those infected drops down to 0.3% as vaccination progresses through the most vulnerable groups, since we’ve heard so many good things about vaccination preventing serious illness even in those who do get ill. This value must also account for the proportion of victims that have not been vaccinated at all, so it’s really a bit of a guess but the right answer has to be significantly lower than the original fatality rate. The loss of immunity in this model occurs on a 1 year time scale, which in practice due to model structure means 1/365 = 0.27% of the immune population return to the vulnerable state each day. I don’t claim these numbers are correct, I merely hope that they are not wrong by a factor of more than about 2. In the long term in the absence of illness, the balance between vaccination and loss of immunity loss would lead to about 1/3rd of the population being vulnerable and 2/3rds being immune at any given time. This is just about enough to permanently suppress the disease (assuming R0=3), or at least keep it at a very low level.

The model simulates the historical trajectory rather well and also matches the ONS and REACT data sets, as I’ve shown previously, so I think it’s broadly reasonable. The recent announcements amount to an opening of schools on the 8th March, and then a subsequent reopening of wider society over the following weeks and months. In the simulations I’m about to present, I’m testing the proposition that we can open up society back to a near-normal situation more quickly. So after bumping the R number up on the 8th March I then increase it again more substantially, putting the underlying R0 number up to 2.5 in the ensemble mean, close to (but still lower than) the value it took at the start of last year, with the intention being to simulate a return to near-normal conditions but with the assumption that some people will still tend to be a bit on the cautious side. So this is a much more ambitious plan than the Govt is aiming for. I’m really just having a look to see what the model does under this fairly severe test. Here is the graph of case numbers when I bump the R number up at the end of April:

And here is the equivalent for deaths, which also shows how the R number rises:

So there is another wave of sorts, but not a terrible one compared to what we’ve seen. In many simulations the death toll does not go over 100 per day though it does go on a long time. Sorry for the messy annotations on the plots, I can’t be bothered adjusting the text position as the run length changes.

If we bring the opening forward to the end of March, it’s significantly worse, due to lower vaccination coverage at that point:

Here the daily deaths goes well over 100 for most simulations and can reach 1000 in the worse cases. On the other hand, if we put off the opening up for another couple of months to the end of July, the picture is very much better, both for cases:

and deaths:

While there are still a few ensemble members generating 100 deaths per day, the median is down at 1, implying a substantial probability that the disease is basically suppressed at that point.

I have to emphasise the large number of simplifications and guesstimates in this modelling. It does however suggest that an over-rapid opening is a significant risk and there are likely benefits to hanging on a bit longer than some might like in order that more people can be vaccinated. My results seems broadly in line with the more sophisticated modelling that was in the media a few days ago. To be honest it’s not far from what you would get out of a back-of-the-envelope calculation based on numbers that are thought to be immune vs vulnerable and the R0 number you expect to arise from social mixing, but for better or worse a full model calculation is probably a bit more convincing.

While the Govt plan seems broadly reasonable to me, there are still substantial uncertainties in how things will play out and it is vitally important that the govt should pay attention to the data and be prepared to shift the proposed dates in the light of evidence that accrues over the coming weeks. Unfortunately history suggests this behaviour is unlikely to occur, but we can live in hope.

BlueSkiesResearch.org.uk: So near and yet not quite…

There’s been quite an amazing turnaround since my last blog post. At the time I wrote that, the Govt was insisting that schools would open as planned (indeed they did open the very next day), and that another lockdown was unthinkable. So my grim simulations were performed on that basis.

Of course, the next evening, we had another u-turn… schools shut immediately and many other restrictions were introduced on social mixing. Even so, most of the experts thought we would be in for a rough time, and I didn’t see any reason to disagree with them. The new variant had been spreading fast and no-one was confident that the restrictions would be enough to suppress it. Vaccination was well behind schedule (who remembers 10 million doses by the end of the year?) and could not catch up exponential growth of the virus.

Just after I posted that blog, someone pointed me to this paper from LSHTM which generated broadly similar results with much more detailed modelling. Their scenarios all predicted about 100k additional deaths in the spring, with the exception of one optimistic case where stiff restrictions starting in mid-December, coupled to very rapid vaccination, could cut this number to 30-40k. Given that we were already in Jan with no lockdown and little vaccination in sight, this seemed out of reach. Here is the table that summarises their projections. Note that their “total deaths” is the total within this time frame, not total for the epidemic.

However, since that point, cases have dropped very sharply indeed. Better than in the most optimistic scenario of LSHTM who anticipated R dropping to a little below 1. Deaths have not peaked quite yet but my modelling predicts this should happen quite soon and then we may see them fall quite rapidly. The future under suppression looks very different to what it did a couple of weeks ago.

So this was the model fit I did back on 3rd Jan, which assumes no lockdown. Left is cases, right is deaths which rises to well over 1k per day for a large part of early 2021.

And here are the cumulative median infections and deaths corresponding to the above, with some grid lines marked on to indicate what was in store up to the end of Feb (for infections) and end of March (for deaths). As you can see, about 100k of the latter in this time frame (ie 186-73 = 113k additional deaths).

Here now are the graphs of the latest model fit showing the extremely rapid drop in cases and predicted drop in deaths assuming a 6 week lockdown:

And here is the resulting median projection for total cumulative infections and deaths as a direct comparison to the previous blog post:

It’s a remarkable turnaround, and looks like we are on track for about 114-86 = 28k additional deaths (to start of April), which is far lower than looked possible a couple of weeks ago. It seems plausible that an large part of the reason for the striking success of the suppression is that the transmission of the new variant was predominantly enhanced in the young and therefore closing schools has had a particularly strong effect. The assumption that lockdown lasts for 6 weeks, and what happens after it, is entirely speculative on my part but I wanted to test how close we were to herd immunity at that point. Clearly there will be more work to be done at that time but it shouldn’t be so devastating as at present, unless we lose all our immunity very rapidly.

So that’s looking much better than it was. However it’s also interesting to think about what might have happened if the Govt had introduced the current restrictions sooner. Moving the start of the lockdown back by three weeks generates the following epidemic trajectory:

and the resulting cumulative infections and deaths look like:

Due to the automatic placing of text it’s not so easy to read but we end up with about 84000 deaths total (to end of March) which is fewer than we’ve already had.

So the additional 30k deaths seems to be the price we paid for Johnson’s determination to battle the experts and save Christmas.

BlueSkiesResearch.org.uk: Not even half-way there

NB: below calculation was made and published on Monday 4th, when schools had just been opened and before the latest lockdown was announced, so we can hope that it is too pessimistic, but the situation is still very challenging.

---

Lots of talk from politicians and others that, while not exactly triumphalist, is certainly very positive and enthusiastic about the prospect of vaccinating ourselves out of trouble. Here’s one of the earliest "light at the end of the tunnel" articles for example. And with the new Oxford/AZ vaccine there is renewed excitement.

Sorry to pour a little bit of cold water on the mood but a bit of perspective is called for.

Here is what my modelling suggests for the progress of the outbreak though the population so far and into the future. It’s not a pretty sight. The total number that may be infected between now and the start of March (less than 2 months away) is more than the entire number that have been infected so far right from the start of the outbreak last Feb/March.

According to these calculations, roughly 15 million have been infected, and a total of roughly 36 million may be by the time it’s over. That is, we have significantly more infections to come, than we have seen so far. And far more than we got in the first wave last spring, when probably something like 10% (my modelling actually says 8%) of the population was infected.

If there ever was a time to stay at home and minimise all unnecessary contact, it most surely is now.

With this rate of spread, vaccinating a few million over the next couple of months has a relatively minor effect. It may reduce the death rate significantly towards the end of this period (and will certainly help the small minority of highly vulnerable people who receive it), but won’t stop the disease spreading widely.

I need to add a few disclaimers about the modelling. This result plotted above is the median of my latest ensemble fit of a simple SEIR model to historical data on deaths and cases. I’ve been modelling the progress of the outbreak for months now and though the model is rather primitive and approximate it has done a pretty decent job of simulating what is actually quite a simple process. If each infected person passes the disease on to more than one other (on average), then the disease grows exponentially, if they pass it on to less than one (on average) then it shrinks exponentially. The more difficult bits (that my model is too simple to attempt) is to predict the effect of specific restrictions such as closing schools or pubs, or determining how many young vs old people get ill. When just looking at total numbers, this simple SEIR model (when carefully used) works better than it probably should.

This simulation, while it fits the historical data well, may not account adequately for the added virulence of the newer strain that has recently emerged. It also assumes that we don’t have an extremely strict lockdown that successfully suppresses the outbreak in the very near future. Reality could end up better than this, or it could end up worse, but I’m pretty confident that the basic message is robust. People are getting infected at a huge rate right now. Stay at home if you can.