BlueSkiesResearch.org.uk: More COVID-19 parameter estimation

The 2 and now 3-segment piecewise constant approach seems to have worked fairly well but is a bit limited. I’m not really convinced that keeping R fixed for such long period and then allowing a sudden jump is really entirely justifiable, especially now we are talking about a more subtle and piecemeal relaxing of controls.

Ideally I’d like to use a continuous time series of R (eg one value per day), but that would be technically challenging with a naive approach involving a whole lot of parameters to fit. Approaches like epi-estim manage to generate an answer of sorts but that approach is based on a windowed local fit to case numbers, and I don’t trust the case data to be reliable. Also, this approach seems pretty bad when there is a sudden change as at lockdown, with the windowed estimation method generating a slow decline in R instead. Death numbers are hugely smoothed compared to infection numbers (due to the long and variable time from infection to death) so I don't think that approach is really viable.

So what I’m trying is a piecewise constant approach, with a chunk length to be determined. I’ll start here with 14 day chunks in which R is held constant, giving us say 12 R values for a 24 week period covering the epidemic (including a bit of a forecast). I choose the starting date to fit the lockdown date into the break between two chunks, giving 4 chunks before and 8 after in this instance.

I’ve got a few choices to make over the prior here, so I’ll show a few different results. The model fit looks ok in all cases so I’m not going to present all of them. This is what we get for the first experiment:

The R values however do depend quite a lot on the details and I’m presenting results from several slightly different approaches in the following 4 plots.

Top right left is the simplest version where each chunk has an independent identically distributed prior for R of N(2,1²). This is an example of the MCMC algorithm at the point of failure, in fact a little way past that point as the 12 parameters aren’t really very well identified by the data. The results are noisy and unreliable and it hasn’t converged very well. The last few values of R here should just sample the prior as there is no constraint at all on them. That they do such a poor job of that is an indication of what a dodgy sample it is. However it is notable that there is a huge drop in R at the right time when the lockdown is imposed, and the values before and after are roughly in the right ballpark. Not good enough, but enough to be worth pressing on with….

Next plot on top right is when I impose a smoothness constraint. R can still vary from block to block, but deviations between neighbouring values are penalised. The prior is still N(2,1²) for each value, so the last values of R trend up towards this range but don’t get there due to smoothness constraint. The result looks much more plausible to me and the MCMC algorithm is performing better too. However, the smoothness constraint shouldn’t apply across the lockdown as there was a large and deliberate change in policy and behaviour at that point.

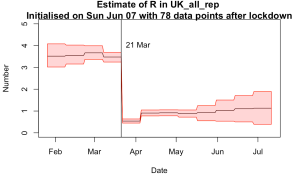
So the bottom left plot has smoothness constraints applied before and after the lockdown but not across it. Note that the pre-lockdown values are more consistent now and the jump at lockdown date is even more pronounced.

Finally, I don’t really think a prior of N(2,1²) is suitable at all times. The last plot uses a prior of N(3,1²) before the lockdown and N(1,0.5²) after it. This is probably a reasonable representation of what I really think and the algorithm is working nicely.

Here is what it generates in terms of daily death numbers:

There is still a bit of of tweaking to be done but I think this is going to be a better approach than the simple 3-chunk version I’ve been using up to now.