Comment on Schwartz

As I hinted, a group of us have taken a more detailed look at Schwartz's paper. It turned out to be quite interesting, in fact, and the results were not exactly as I had anticipated in my first glance.

In a nutshell, Schwartz assumes the climate system can be reasonably approximated as the simplest zero-dimensional energy balance model forced by white noise plus an anthropogenic trend, and further that the relevant parameters of this model (time scale and heat capacity) can be estimated from observed time series of surface temperature and ocean heat content.

There's a detailed post up at RealClimate which mostly focusses on the inapplicability of this energy balance model assumption - I'm sure that even Schwartz would admit this is at best an approximation, and contrary to his claims, the data clearly don't look like they come from such a system. Therefore, the whole concept of a single "time scale" which describes the relaxation rate of the climate system to any and all changes in forcing is rather suspect at the outset.

However, we also found the rather interesting (to me) effect:

Even if the climate system really was a simple energy balance model, the estimation method gives highly inaccurate and strongly biased answers anyway!

This came as a completely surprise - in my first post, I just assumed that the time series analysis method was well-known and gave accurate results as claimed. But it's simply not true.

I was right in assuming that the method for estimating the parameters of autoregressive processes was well established. What is also well established is that these estimates are biased, sometimes strongly so. Bartlett's Formula (which dates back to 1946) says that the sample estimate of the lag-1 autocorrelation parameter of a finite time series generated by an AR1 process converges to a random sample from N(r,sqrt((1-r²)/n)) as n (sample length) tends to infinity - that is, the distribution of samples converges to a Gaussian distribution centred on the true value, with a reasonably narrow width. But this is the asymptotic distribution for large n, not the actual distribution for a specific finite n.

The observational time series of annual average global surface temperature as used by Schwartz has 125 points. If the real time scale was 30 years, then that means the AR1 parameter r=exp(-1/30) is 0.967, and so Bartlett's Formula says the estimate should look like a sample from N(0.967, 0.02). This has a 95% probability interval of about 0.92 - 1 (actually the formula goes above 1, but this is a hard upper limit for the observed sample correlation). However, there is also a long literature (dating back to Orcutt 1948, only 2 years later than Bartlett's original paper) observing that there is a bias in the estimate. For the example above, the actual results obtained from Monte Carlo sampling have a 95% range of 0.82 - 0.97 with a median of 0.93. Someone has actually produced a formula for the bias of the mean, which is given by -(1+4r)/n, or about -0.04 in this case. This agrees well with our experimental results, but the much larger uncertainty (compared to Bartlett's Formula) is also worth noting.

Here's a graphical representation of that point. The blue curve shows the anticipated results according to Bartlett's formula for the case r=0.967, n=125. The red histogram shows the results that are obtained in practice for the sample lag-1 autocorrelation of AR1 series with the same parameters.

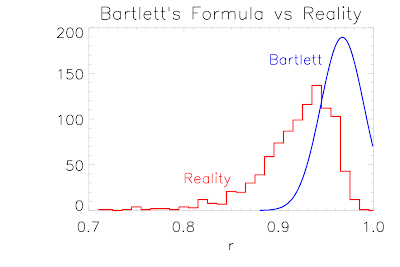That result is just for the first lag, but similar results can be obtained for higher lags too.

When turned back into a time scale (via tau = -1/log(r)), the 95% probability interval of Bartlett's formula ranges from 12 up to infinity. So that's quite a wide range, but at least it is centred on the true answer of 30y and it doesn't get very close to 5y (due to the log transform, 12 is a long way from 5). But the 95% probability interval of the experimental answer ranges from 5 to 36 years with a median of 13! So it's hugely biased and barely reaches the true value.

In the submitted comment we show the results from a set of experiments with the simple energy balance model that Schwartz uses. Whether we use realistic forcing and detrend the results as Schwartz did (upper panel) or just white noise with no detrending (which results in a pure AR1 series, giving the results shown in the lower panel) the results are basically the same. In all cases, if the intrinsic time scale of the model is long, there is a strong bias in the estimate and observing a result as low as 5y is quite plausible even for a true time scale of 30y (corresponding to a sensitivity of 6C for doubled CO2) or more. Again, these results are insensitive to various details such as the amount of noise added and which lags are examined.


We also looked briefly at the outputs from the IPCC AR4 models, which are shown in the top panel. When applied to their simulations of the 20th century, the method returns a "time scale" that is much lower than the true relaxation time scale of the models which is known to be of the order of decades. Assuming a plausible heat capacity (and we don't fault Schwartz on that), these erroneous "time scale" estimates will generate unreasonably low estimates of climate sensitivity. This was thoroughly checked with an ensemble of GISS model runs, the analysis of which did as expected generate strongly biased estimates of sensitivity (3-20 times too low compared to the real answer). We didn't wade through the mountain of data necessary to check this with all models but the IPCC AR4 already says that they generally mix too much heat into the ocean (meaning a high heat capacity) so it is clear that this method will tend to generate strongly biased estimates for them too.

In conclusion, even if it was reasonable to approximate the climate system by a simple energy balance system (which the data refute) then Schwartz's estimate of 5+-1y for the time scale is not supported by the analysis - the estimation method is intrinsically biased and much more uncertain than his numbers suggest. In a wide range of numerical experiments where the time scale is known, the time series analysis gets it badly wrong. In short, this "time scale" analysis does not generate a useful diagnostic.

Some people have suggested that Schwartz didn't really believe his result, he was just putting it out to be shot down. Well, he has been touting this for some time - here is his abstract from the AGU meeting last year. and the manuscript has apparently been doing the rounds too. In fact another climate scientist contacted me through email to say that he'd tried to explain that it was wrong, and got nowhere, but perhaps he did not find as compelling a criticism as we think we have produced. So I was wrong to presume that Schwartz hadn't spoken to anyone in the field, but there is not much point in talking to people if you are then just going to ignore them! Based on my limited email interaction, Schwartz still seems convinced he is on to something that the rest of the world has overlooked. But we will have to wait and see how he responds in writing.