Implicit priors and the energy balance of the earth system

So, this old chestnut seems to keep on coming back....

Back in 2002, Gregory et al proposed that we could generate “An observationally based estimate of the climate sensitivity” via the energy balance equation S = F_2x dT/Q where S is the equilibrium sensitivity to 2xCO2, F_2x = 3.7 is the (known constant) forcing of 2xCO2, dT is the observed surface air temperature change and Q is the net radiative imbalance at the surface which takes account of both radiative forcing and the deep ocean heat uptake. (Their notation is marginally different, I'm simplifying a bit.)

Observational values for both dT and Q can be calculated/observed, albeit with uncertainties (reasonably taken to be Gaussian). Repeatedly sampling from these observationally-derived distributions and taking the ratio generates an ensemble of values for S which can be used as a probability distribution. Or can it? Is there a valid Bayesian interpretation of this, and if so, what was the prior for S? Because we know that it is not possible to generate a Bayesian posterior pdf from observations alone. And yet, it seems that one was generated.

This method may date back to before Gregory et al, and is still used quite regularly. For example, Thorsten Mauritsen (who we were visiting in Hamburg recently) and Robert Pincus did it in their recent “Committed warming” paper. Using historical observations, they generated a rather tight estimate for S as 1.1-4.4C, though this wasn't really the main focus of their paper. It seems a bit optimistic compared to much of the literature (which indicates the 20th century to provide a rather weaker constraint than that) so what's the explanation for this?

The key is in the use of the observationally-derived distributions for the quantities dT and Q. It seems quite common among scientists to interpret a measurement x_o of an unknown x, with some known (or perhaps assumed) uncertainty σ, as implying the probability distribution N(x_o,σ) for x. However, this is not justifiable in general. In Bayesian terms, it may be considered equivalent to starting with a uniform prior for x and updating with the likelihood arising from the observation. In many cases, this may be a reasonable enough thing to do, but it's not automatically correct. For instance, if x is known to be positive definite, then the posterior distribution must be truncated at 0, making it no longer Gaussian (even if only to a negligible degree). (Note however that it is perfectly permissible to do things like use (x_o - 2σ, x_o + 2σ) as a 95% frequentist confidence interval for x, even when it is not a reasonable 95% Bayesian credible interval. Most scientists don't really understand the distinction between confidence intervals and credible intervals, which may help to explain why the error is so prevalent.)

So by using the observational estimates for dT and Q in this way, the researcher is implicitly making the assumption of independent uniform priors for these quantities. This implies, via the energy balance equation, that their prior on S is the quotient of two uniform priors. Which has a funny shape in general, with a flat region near 0 and then a quadratically-decaying tail. Moreover, this prior on S is not independent of the prior for either dT or Q. Although it looks like there are three unknown quantities, the energy balance equation tying them together means there are only two degrees of freedom here.

At the time of the IPCC AR4, this rather unconventional implicit prior for S was noticed by Nic Lewis who engaged in some correspondence with IPCC authors about the description and presentation of the Gregory et al results in that IPCC report. His interpretation and analysis is very sightly different to mine, in that he took the uncertainty in dT to be so (relatively) small that one could ignore it and consider the uniform prior on Q alone, which implies an inverse quadratic prior on S. However the principle of his analysis is similar enough.

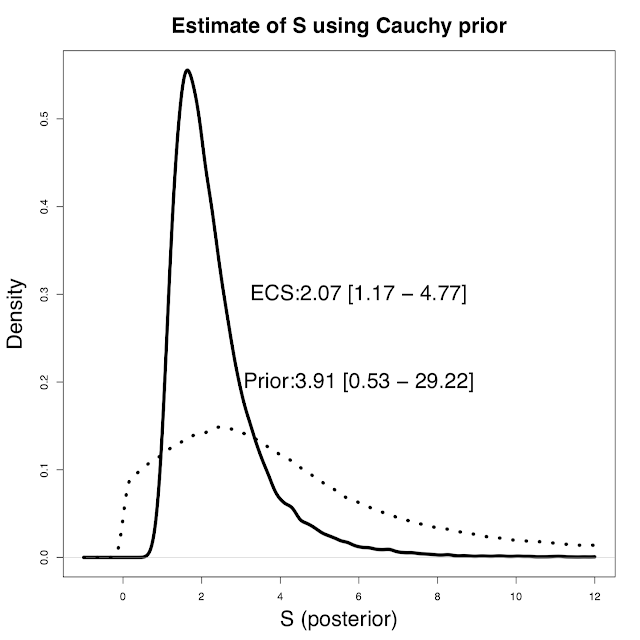
In my opinion, a much more straightforward and natural way to approach the problem is instead to define the priors over Q and S directly. These can be whatever we want and are prepared to defend publicly. I've previously advocated a Cauchy prior for S which avoids the unreasonableness and arbitrariness of a uniform prior for this constant. In contrast, a uniform prior over Q (independent of S) is probably fairly harmless in this instance, and this does allow for directly using the observational estimate of Q as a pdf. Sampling from these priors to generate an ensemble of (S,Q) pairs allows us to calculate the resulting dT and weight the ensemble members according to how well the simulated values match the observed temperature rise. This is standard Monte Carlo integration using Bayes Theorem to update a prior with a likelihood. Applying this approach to Thorsten's data set (and using my preferred Cauchy prior), we obtain a slightly higher range for S of 1.2 - 4.8C. Here's a picture of the results (oops, ECS = S there, an inconsistent labelling that I can't be bothered fixing).

The median and 5-95% ranges for prior and posterior are also given. As you can see, the Cauchy prior doesn't really cut off the high tail that aggressively. In fact it's a lot higher than a U[0,10] or even U[0,20] prior would imply.