The Govt changed the lockdown rules substantially from the 4th July, with pubs, restaurants reopening and a new “1m plus” rule to replace the previous 2m distancing requirement. Predictably, the tabloids announced a new free-for-all which they labelled “Independence day”.
Up to this time, the R number had been fairly stable at around 0.8, meaning that each infected person would pass the disease onto less than one person on average and the rate of illness (and death) was dropping fairly steadily at about 20% reduction per week.
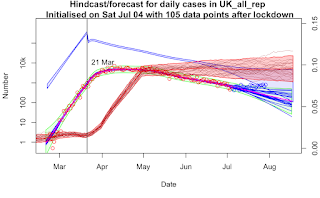
Below is how my model fits to the data up to 4th July (red circles in both plots). You can click on the plots for bigger and clearer versions. The left hand plot is daily reported cases, and the right hand plot is daily deaths. The green plume shows the model fit to each of these, with a few lines from the ensemble drawn on (dark blue) and the median prediction in magenta. The thin blue plume is the total modelled number of new infections each day, which is much higher. There is also a red plume on this plot representing the “case ascertainment factor”, ie the proportion of infections that is actually observed. This uses the scale on the right hand side of the plot, and so rises from about 1% at the start of the epidemic, to around 10% now. The blue circles represent data that had not been observed by the 4th July, and you can see in the LH plot that they tend to drift above the model forecast.
On the right hand plot, the red plume is the R number (which again uses the axis on the right hand side of that plot). It starts off around 3ish, then drops sharply when the lockdown controls were imposed, and wobbles around a bit after that point. The “current” number quoted there (mean and range) is the estimate as of the 4th July. The data observed subsequent to that date agree better with the model than was the case in the LH plot, but still look to be more above than below the forecast.
Redoing the analysis as of yesterday's data (i.e. including all data points in the estimation), and we get the following:
Now the rise in cases is reflected in the LH graph, and the corresponding rise in R is shown at the bottom of the RH plot. R is probably greater than 1, meaning that the epidemic is starting to take off again. It seems that something happened around the 4th of July to increase the rate of infection. I wonder what that could have been?
So, emboldened by these results and Peter's comment below we can try adding in a step change on the 4th July - this is just a high variance step in the prior, I'm not imposing a rise specifically, just allowing a large change. This generates the result below and it looks like a rather better fit especially to cases. However I'm not really that confident about what is going to happen and especially wouldn't be surprised if there is a bit of a decoupling between cases and deaths due to differences in the age range of people infected (eg mostly younger working age with a much lower fatality rate).





12 comments:
I think it is more than just the UK ...
https://live.staticflickr.com/65535/50169300223_a1c526b074_b.jpg
Both the UK and the EU may have reached noise floors. It is rather clear that the number of confirmed cases are now increasing for both.
Fact is we never had much headroom with such a transmissible disease and have done well to keep it suppressed for so long, especially with such a poor testing and tracing system (which has to be fast and comprehensive to work).
The change from easing lockdown looks to be much more spread out than the change at imposition of lockdown? Is that built into your priors - i.e. you allow for a step change in March but not July? Or does it emerge naturally from the shape of the data?
Thank goodness there's no risk of mutations that will increase transmissibility.
>more than just the UK
So with many countries showing the same do you conclude that a) virus has become more infectious and little to do with relaxing lockdown.
b) EU countries are now finding more of the milder cases, or
c) EU governments can't afford to support the economy during the long shutdown needed to eliminate the long tail so they are all relaxing lockdown too much, too soon.
b) is the optimistic version. Growth in cases would be expected to look more linear than exponential growth.
a) is pessimistic and I don't see evidence for this whereas evidence the other way includes timing of change in UK and some countries leveling off after large second wave suggesting lockdown measures brought back in.
c) looks overwhelming the likely dominant option when you look at the pattern of growth in various EU countries:
July regrowth
Looking more like exponential growth than linear: Belgium, Bulgaria, Croatia, Cyprus (perhaps not enough data), Czech Republic, France (long period of steady growth but recently more rapid - perhaps ambiguous), Greece, Luxemboug, Netherlands, Poland (not much data but rapid growth), Romania, Slovakia, Slovenia, Spain.
Linear or less than linear growth: Austria (maybe a step up then not enough data after that),
Not enough time after rise starts to get impression of linear or exponential: Denmark, Germany (recent more rapid but perhaps ambiguous), Ireland, Italy, Latvia, Lithuania, Malta (rapid recent growth but little data), Switzerland, UK
Doesn't follow pattern of first peak April/May, low in June, then growing again: Estonia, Finland, Hungary, Portugal, Sweden.
Some classifications may well be disputable .... but when I come to 14:1 in favour of looking more like exponential growth pattern than linear then I feel comfortable saying that seems the dominant pattern.
c looks more supported by the evidence but this was my gut reaction (with a little bit of hoping for b) so maybe I am just seeing the evidence to support my gut reaction and fears.
Yes Peter that is just due to the form of the prior, which only allows for gradual changes (other than at lockdown). I have now added a bigger step and updated the post. There is no way to diagnose a specific date of change though, the data is far too smooth and delayed for that.
Are you aiming to make the code available sometime? I sure there are people wanting to investigate what this would show in places like Texas, Florida, etc.
"Last updated on Friday 31 July 2020.
Latest R number range for the UK
0.8-0.9"
https://www.gov.uk/guidance/the-r-number-in-the-uk#history
When do you think Sage will catch up with you?
>"especially wouldn't be surprised if there is a bit of a decoupling between cases and deaths due to differences in the age range of people infected (eg mostly younger working age with a much lower fatality rate)."
There is substantial delay before deaths follow cases. An intermediate data set is to look at hospital admissions:
https://coronavirus-staging.data.gov.uk/healthcare
Hopefully less delay between confirmed cases and hospitalization than between confirmed cases and deaths. While this might somewhat avoid the problem of getting better at finding milder cases, I suspect this will as you suggest be swamped by age range and medical complications of people infected.
Hospitalizations still seem to be going down.
If there is a difference, then there is question of whether government should aim to
a) Maximize economic activity while keeping cases from going up, or
b) Maximize economic activity while keeping hospitalizations from going up.
If the endgame is: elimination only really possible when vaccination is widely available, then perhaps getting sufficient immunity in the population is easier if cases have been allowed to go high while hospitalizations limited rather than keeping both cases and hospitalizations low?
A long time before vaccinations available might make this approach inappropriate, cases will eventually spread from younger to older age groups in the population. I suspect this would be a politically risky strategy.
Calculating an expected number of total cases from hospitalizations adjusted for age might be interesting to compare with confirmed cases in order to see if there is any detectable trend in getting better at finding milder cases?
Your R may be too high if we are getting better at finding milder cases and being able to adjust for that might be useful?
That SAGE assessment is shocking. I note that they don't believe it themselves, if you read the small print. What a bunch of jokers.
It seems clear that pretty much everywhere, countries are catching the rise in cases well ahead of deaths. I keep on expecting to run up against the limitations of my simple model but it's doing ok so far...
Phil,
I suppose I ought to. If I knew of a cheap/free route to publication I'd be more tempted but had a pretty shit experience so far which has put me off. I also got a bit distracted from the whole publication thing due to real (unrelated) work intervening. And also I got a bit bored by it. I don't know. The experts are also starting to work it out themselves, though I think they still haven't got a method quite as good as mine...
Well if you decide that you are NOT publishing, then putting up the code on Github would be a service to mankind.
Post a Comment